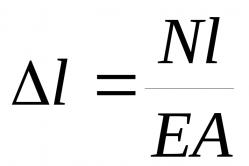8.2. Основни закони, използвани в съпротивлението на материалите

Статични отношения. Те се записват под формата на следните уравнения на равновесието.

Закон на Хук ( 1678): колкото по-голяма е силата, толкова по-голяма е деформацията и освен това е право пропорционална на силата. Физически това означава, че всички тела са пружини, но с голяма твърдост. Когато една греда е просто опъната от надлъжна сила н= Етози закон може да се напише като:

Тук
надлъжна сила, л- дължина на лъча, А- неговата площ на напречното сечение, д- коефициент на еластичност от първи род ( Модул на Юнг).

Като се вземат предвид формулите за напрежения и деформации, законът на Хук е написан, както следва:
.

Подобна връзка се наблюдава при експерименти между тангенциалните напрежения и ъгъла на срязване:

.

Ж Нареченмодул на срязване , по-рядко – модул на еластичност от втори род. Като всеки закон, законът на Хук също има граница на приложимост. Волтаж
, до която е валиден законът на Хук, се нарича граница на пропорционалност(това е най-важната характеристика за здравина на материалите).

Нека изобразим зависимостта  от  графично (фиг. 8.1). Тази снимка се нарича диаграма на разтягане . След точка Б (т.е
) тази зависимост престава да бъде линейна.

При
след разтоварване се появяват остатъчни деформации в тялото, следователно Наречен граница на еластичност .

Когато напрежението достигне стойността σ = σ t, много метали започват да проявяват свойството, наречено течливост. Това означава, че дори при постоянно натоварване материалът продължава да се деформира (т.е. държи се като течност). Графично това означава, че диаграмата е успоредна на абсцисата (участък DL). Напрежението σ t, при което тече материалът, се нарича провлачване .

Някои материали (St. 3 - строителна стомана) след кратко течение започват отново да се съпротивляват. Съпротивлението на материала продължава до определена максимална стойност σ pr, след което започва постепенно разрушаване. Величината σ пр се нарича издръжливост на опън (синоним на стомана: якост на опън, за бетон - кубична или призматична якост). Използват се и следните обозначения:

=Р b

Подобна връзка се наблюдава при експерименти между напреженията на срязване и срязването.

3) Закон на Дюамел–Нойман (линейно термично разширение):

При наличие на температурна разлика телата променят размерите си и то правопропорционално на тази температурна разлика.

Нека има температурна разлика
. Тогава този закон изглежда така:

Тук α - коефициент на линейно термично разширение, л - дължина на пръта, Δ л- неговото удължаване.

4) Закон за пълзенето .

Изследванията показват, че всички материали са силно разнородни в малки площи. Схематичната структура на стоманата е показана на фиг. 8.2.

Някои от компонентите имат свойствата на течност, така че много материали под натоварване получават допълнително удължение с течение на времето
(фиг. 8.3.) (метали при високи температури, бетон, дърво, пластмаси - при нормални температури). Това явление се нарича пълзенематериал.

Законът за течностите е: колкото по-голяма е силата, толкова по-голяма е скоростта на движение на тялото в течността. Ако тази зависимост е линейна (т.е. силата е пропорционална на скоростта), тогава тя може да се запише като:

д
Ако преминем към относителните сили и относителните удължения, получаваме

Ето индекса " кр "означава, че се взема предвид частта от удължението, причинена от пълзенето на материала. Механични характеристики наречен коефициент на вискозитет.

Закон за запазване на енергията.

Помислете за натоварена греда

Нека въведем концепцията за преместване на точка, например,

- вертикално движение на точка B;

- хоризонтално изместване на точка С.

правомощия
докато върши някаква работа U. Като се има предвид, че силите
започват да нарастват постепенно и приемайки, че те нарастват пропорционално на изместванията, получаваме:

.

Според закона за опазване: нито една работа не изчезва, тя се изразходва за извършване на друга работа или се превръща в друга енергия (енергия- това е работата, която тялото може да извърши.).

Работа на силите
, се изразходва за преодоляване на съпротивлението на еластичните сили, възникващи в тялото ни. За да изчислим тази работа, ние вземаме предвид, че тялото може да се счита, че се състои от малки еластични частици. Нека разгледаме един от тях:

Той е обект на напрежение от съседни частици . Полученият стрес ще бъде

Под влиянието частицата ще се удължи. Според дефиницията, удължението е удължението за единица дължина. Тогава:

Нека изчислим работата dW, което силата прави dN (тук също така се взема предвид, че силите dNзапочват да нарастват постепенно и нарастват пропорционално на движенията):

За цялото тяло получаваме:

.

работа Укоето беше извършено , Наречен енергия на еластична деформация.

Според закона за запазване на енергията:

6)Принцип възможни движения .

Това е един от вариантите за написване на закона за запазване на енергията.

Нека силите действат върху гредата Е 1 , Е 2 , … . Те карат точките да се движат в тялото
и напрежение
. Да дадем тялото допълнителни малки възможни движения
. В механиката, обозначение на формата
означава фразата „възможна стойност на количеството А" Тези възможни движения ще предизвикат тялото възможни допълнителни деформации
. Те ще доведат до появата на допълнителни външни сили и напрежения
, δ.

Нека изчислим работата на външните сили върху допълнителни възможни малки премествания:

Тук
- допълнителни движения на тези точки, в които се прилагат сили Е 1 , Е 2 , …

Помислете отново за малък елемент с напречно сечение dA и дължина дз (виж фиг. 8.5. и 8.6.). Според дефиницията допълнително удължение  дзна този елемент се изчислява по формулата:

дз=  дз.

Силата на опън на елемента ще бъде:

dN = (+δ) dA ≈  dA..

Работата на вътрешните сили върху допълнителните премествания се изчислява за малък елемент, както следва:

dW = dN  dz = dA dz =  dV

СЪС
сумирайки енергията на деформация на всички малки елементи, получаваме общата енергия на деформация:

Закон за запазване на енергията У = Uдава:

.

Това съотношение се нарича принцип на възможните движения(нарича се още принцип на виртуалните движения).По същия начин можем да разгледаме случая, когато действат и тангенциални напрежения. Тогава можем да получим това за енергията на деформация Уще бъде добавен следният термин:

Тук  е напрежението на срязване,  е преместването на малкия елемент. Тогава принцип на възможните движенияще приеме формата:

За разлика от предишната форма на записване на закона за запазване на енергията, тук няма предположение, че силите започват да нарастват постепенно и те нарастват пропорционално на преместванията

7) Ефект на Поасон.

Нека разгледаме модела на удължаване на пробата:

Феноменът на скъсяване на елемент на тялото в посока на удължаване се нарича Ефект на Поасон.

Нека намерим надлъжната относителна деформация.

Относителната напречна деформация ще бъде:

Коефициент на Поасонколичеството се нарича:

За изотропни материали (стомана, чугун, бетон) коефициент на Поасон

Това означава, че в напречна посока деформацията по-малконадлъжно

Забележка : съвременните технологии могат да създават композитни материали с коефициент на Поасон >1, тоест напречната деформация ще бъде по-голяма от надлъжната. Например, такъв е случаят с материал, подсилен с твърди влакна под нисък ъгъл
<<1 (см. рис.8.8.). Оказывается, что коэффициент Пуассона при этом почти пропорционален величине
, т.е. по-малкото , толкова по-голям е коефициентът на Поасон.

Фиг.8.8. Фиг.8.9

Още по-изненадващ е материалът, показан на (Фиг. 8.9.), а за такава армировка има парадоксален резултат - надлъжното удължаване води до увеличаване на размера на тялото в напречна посока.

8) Обобщен закон на Хук.

Нека разгледаме елемент, който се простира в надлъжна и напречна посока. Нека намерим деформацията, която възниква в тези посоки.

Нека изчислим деформацията произтичащи от действие :

Нека разгледаме деформацията от действието , който възниква в резултат на ефекта на Поасон:

Общата деформация ще бъде:

Ако е валидно и , тогава ще бъде добавено още едно скъсяване по посока на оста x
.

Следователно:

По същия начин:

Тези отношения се наричат обобщен закон на Хук.

Интересно е, че когато се пише законът на Хук, се прави предположение за независимостта на деформациите на удължение от деформациите на срязване (за независимост от напреженията на срязване, което е едно и също нещо) и обратно. Експериментите добре потвърждават тези предположения. Гледайки напред, отбелязваме, че силата, напротив, силно зависи от комбинацията от тангенциални и нормални напрежения.

Забележка: Горните закони и предположения се потвърждават от многобройни преки и косвени експерименти, но, както всички други закони, те имат ограничен обхват на приложение.

Както знаете, физиката изучава всички закони на природата: от най-простите до най-общите принципи на естествената наука. Дори в тези области, където изглежда, че физиката не е в състояние да разбере, тя все пак играе първостепенна роля и всеки най-малък закон, всеки принцип - нищо не ѝ убягва.

Във връзка с

Физиката е в основата на основите, тя лежи в началото на всички науки.

Физика изучава взаимодействието на всички тела,едновременно парадоксално малки и невероятно големи. Съвременната физика активно изучава не просто малки, а хипотетични тела и дори това хвърля светлина върху същността на Вселената.

Физиката е разделена на раздели,това опростява не само самата наука и нейното разбиране, но и методологията на изследване. Механиката се занимава с движението на телата и взаимодействието на движещите се тела, термодинамиката се занимава с топлинните процеси, електродинамиката се занимава с електрическите процеси.

Защо механиците трябва да изучават деформацията?

Когато говорим за компресия или напрежение, трябва да си зададете въпроса: кой клон на физиката трябва да изучава този процес? При силни изкривявания може да се отдели топлина, може би термодинамиката трябва да се справи с тези процеси? Понякога при компресиране на течности започва да кипи, а при компресиране на газове се образуват течности? И така, трябва ли хидродинамиката да разбира деформацията? Или молекулярно-кинетична теория?

Всичко зависи от от силата на деформация, от нейната степен.Ако деформируемата среда (материал, който се компресира или разтяга) позволява и компресията е малка, има смисъл да се разглежда този процес като движение на някои точки на тялото спрямо други.

И тъй като въпросът е чисто свързан, значи механиците ще се занимават с него.

Законът на Хук и условията за неговото изпълнение

През 1660 г. известният английски учен Робърт Хук открива явление, което може да се използва за механично описание на процеса на деформация.

За да разберем при какви условия е изпълнен законът на Хук, Нека се ограничим до два параметъра:

• сряда;
• сила.

Има среди (например газове, течности, особено вискозни течности, близки до твърди състояния или, обратно, много течни течности), за които е невъзможно процесът да се опише механично. Обратно, има среди, в които при достатъчно големи сили механиката спира да „работи“.

важно!На въпроса: „При какви условия законът на Хук е верен?“ Може да се даде категоричен отговор: „При малки деформации“.

Закон на Хук, определение: Деформацията, която възниква в тялото, е право пропорционална на силата, която причинява тази деформация.

Естествено, това определение предполага, че:

• компресията или разтягането са малки;
• еластичен предмет;
• състои се от материал, в който няма нелинейни процеси в резултат на компресия или опън.

Законът на Хук в математическа форма

Формулировката на Хук, която цитирахме по-горе, дава възможност да я напишем в следната форма:

където е промяната в дължината на тялото поради компресия или разтягане, F е силата, приложена към тялото и причиняваща деформация (еластична сила), k е коефициентът на еластичност, измерен в N/m.

Трябва да се помни, че законът на Хук важи само за малки участъци.

Отбелязваме също, че има същия външен вид, когато се разтяга и компресира. Като се има предвид, че силата е векторна величина и има посока, тогава в случай на компресия следната формула ще бъде по-точна:

Но отново всичко зависи от това накъде ще бъде насочена оста, спрямо която измервате.

Каква е основната разлика между компресия и разширение? Нищо, ако е незначително.

Степента на приложимост може да се разглежда, както следва:

Нека обърнем внимание на графиката. Както виждаме, при малки участъци (първата четвърт от координатите), за дълго време силата с координатата има линейна връзка (червена линия), но след това реалната връзка (пунктирана линия) става нелинейна и законът престава да е истина. На практика това се отразява чрез толкова силно разтягане, че пружината спира да се връща в първоначалното си положение и губи свойствата си. С още повече разтягане настъпва счупване и конструкцията се срутваматериал.

При малки компресии (трета четвърт от координатите) дълго време силата с координатата също има линейна връзка (червена линия), но след това истинската връзка (пунктирана линия) става нелинейна и всичко спира да работи отново. На практика това води до толкова силна компресия, че започва да се отделя топлинаи пружината губи свойствата си. При още по-голяма компресия намотките на пружината се „залепват“ и тя започва да се деформира вертикално и след това напълно се стопява.

Както можете да видите, формулата, изразяваща закона, ви позволява да намерите силата, като знаете промяната в дължината на тялото, или, като знаете еластичната сила, да измерите промяната в дължината:

Също така в някои случаи можете да намерите коефициента на еластичност. За да разберете как се прави това, разгледайте примерна задача:

Към пружината е свързан динамометър. Той беше разтегнат чрез прилагане на сила 20, поради което стана дълъг 1 метър. След това я пуснаха, изчакаха докато вибрациите спрат и тя се върна в нормалното си състояние. В нормално състояние дължината му беше 87,5 сантиметра. Нека се опитаме да разберем от какъв материал е направена пружината.

Нека намерим числената стойност на деформацията на пружината:

От тук можем да изразим стойността на коефициента:

Разглеждайки таблицата, можем да открием, че този индикатор съответства на пружинната стомана.

Проблем с коефициента на еластичност

Физиката, както знаем, е много прецизна наука, освен това е толкова прецизна, че е създала цели приложни науки, които измерват грешките. Модел на непоколебима прецизност, тя не може да си позволи да бъде тромава.

Практиката показва, че линейната зависимост, която разгледахме, не е нищо повече от Закон на Хук за тънък и опънат прът.Само по изключение може да се използва за пружини, но и това е нежелателно.

Оказва се, че коефициентът k е променлива стойност, която зависи не само от материала, от който е направено тялото, но и от диаметъра и неговите линейни размери.

Поради тази причина нашите заключения изискват пояснение и развитие, защото в противен случай формулата:

може да се нарече нищо повече от зависимост между три променливи.

Модул на Юнг

Нека се опитаме да намерим коефициента на еластичност. Този параметър, както разбрахме, зависи от три величини:

• материал (който ни устройва доста);
• дължина L (което показва зависимостта му от);
• площ С.

важно!Така, ако успеем по някакъв начин да „отделим“ дължината L и площта S от коефициента, тогава ще получим коефициент, който напълно зависи от материала.

Какво знаем:

• колкото по-голяма е площта на напречното сечение на тялото, толкова по-голям е коефициентът k и зависимостта е линейна;
• колкото по-дълго е тялото, толкова коефициентът k е по-нисък, а зависимостта е обратно пропорционална.

Това означава, че можем да запишем коефициента на еластичност по следния начин:

където E е нов коефициент, който сега зависи точно от вида на материала.

Нека въведем понятието „относително удължение“:

. 

Заключение

Нека формулираме закона на Хук за опън и компресия: При малки компресии нормалното напрежение е право пропорционално на удължението.

Коефициентът E се нарича модул на Юнг и зависи единствено от материала.

Наблюденията показват, че за повечето еластични тела, като стомана, бронз, дърво и др., големината на деформациите е пропорционална на големината на действащите сили. Типичен пример, обясняващ това свойство, е пружинен баланс, при който удължението на пружината е пропорционално на действащата сила. Това се вижда от факта, че скалата на разделяне на такива везни е еднаква. Като общо свойство на еластичните тела, законът за пропорционалност между сила и деформация е формулиран за първи път от Р. Хук през 1660 г. и публикуван през 1678 г. в работата „De potentia restitutiva“. В съвременната формулировка на този закон не се разглеждат силите и движенията на точките на тяхното приложение, а напрежението и деформацията.

Така за чисто напрежение се приема:

Това е относителното удължение на всеки сегмент, взет в посоката на разтягане. Например, ако ребрата, показани на фиг. 11 призмите преди прилагане на натоварването са били a, b и c, както е показано на чертежа, а след деформация те ще бъдат съответно, тогава .

Константата E, която има размерността на напрежението, се нарича модул на еластичност или модул на Юнг.

Напрежението на елементите, успоредни на действащите напрежения o, се придружава от свиване на перпендикулярни елементи, т.е. намаляване на напречните размери на пръта (размери на чертежа). Относителна напречна деформация

ще бъде отрицателна стойност. Оказва се, че надлъжните и напречните деформации в еластично тяло са свързани с постоянно съотношение:

Безразмерното количество v, постоянно за всеки материал, се нарича коефициент на странично сгъстяване или коефициент на Поасон. Самият Поасон, изхождайки от теоретични съображения, които по-късно се оказват неверни, вярва, че за всички материали (1829 г.). Всъщност стойностите на този коефициент са различни. Да, за стомана

Заменяйки израза в последната формула, получаваме:

Законът на Хук не е точен закон. За стоманата отклоненията от пропорционалността между са незначителни, докато чугунът или резбата явно не се подчиняват на този закон. За тях и може да се апроксимира с линейна функция само в най-грубото приближение.

Дълго време якостта на материалите се занимаваше само с материали, които се подчиняват на закона на Хук, и прилагането на формулите за якост на материалите към други тела можеше да се направи само с голяма резерва. Понастоящем нелинейните закони за еластичност започват да се изучават и прилагат за решаване на конкретни проблеми.

Закон на Хукобикновено наричани линейни зависимости между компонентите на напрежението и компонентите на напрежението.

Да вземем елементарен правоъгълен паралелепипед с лица, успоредни на координатните оси, натоварен с нормално напрежение σ x, равномерно разпределени върху две срещуположни лица (фиг. 1). При което σy = σ z = τ x y = τ x z = τ yz = 0.

До границата на пропорционалност относителното удължение се дава по формулата

Където д— модул на еластичност на опън. За стомана д = 2*10 5 MPa, следователно деформациите са много малки и се измерват като процент или 1 * 10 5 (в тензодатчици, които измерват деформации).

Удължаване на елемент в посоката на оста хпридружено от нейното стесняване в напречна посока, обусловено от деформационните компоненти

Където μ - константа, наречена коефициент на странично сгъстяване или коефициент на Поасон. За стомана μ обикновено се приема за 0,25-0,3.

Ако въпросният елемент е натоварен едновременно с нормални напрежения σ x, σy, σ z, равномерно разпределени по стените му, след което се добавят деформации

Чрез наслагване на компонентите на деформация, причинени от всяко от трите напрежения, получаваме отношенията

Тези връзки се потвърждават от множество експерименти. Приложено метод на наслагванеили суперпозициинамирането на общите деформации и напрежения, причинени от няколко сили, е легитимно, докато деформациите и напреженията са малки и линейно зависими от приложените сили. В такива случаи пренебрегваме малки промени в размерите на деформираното тяло и малки движения на точките на прилагане на външни сили и базираме изчисленията си на първоначалните размери и първоначалната форма на тялото.

Трябва да се отбележи, че малките премествания не означават непременно, че връзките между силите и деформациите са линейни. Така, например, в компресирана сила Qпрът, натоварен допълнително със сила на срязване Р, дори и с малка деформация δ възниква допълнителен момент М = Qδ, което прави проблема нелинеен. В такива случаи общите деформации не са линейни функции на силите и не могат да бъдат получени чрез проста суперпозиция.

Експериментално е установено, че ако напреженията на срязване действат по всички страни на елемента, тогава изкривяването на съответния ъгъл зависи само от съответните компоненти на напрежението на срязване.

Константа Жнаречен модул на еластичност на срязване или модул на срязване.

Общият случай на деформация на елемент поради действието на три нормални и три тангенциални компоненти на напрежение върху него може да се получи чрез суперпозиция: три деформации на срязване, определени от съотношения (5.2b), се наслагват върху три линейни деформации, определени от изрази ( 5.2а). Уравнения (5.2a) и (5.2b) определят връзката между компонентите на деформациите и напреженията и се наричат обобщен закон на Хук. Нека сега покажем, че модулът на срязване Жизразено чрез модул на еластичност на опън ди коефициент на Поасон μ . За да направите това, разгледайте специалния случай, когато σ x = σ , σy = -σ И σ z = 0.

Нека изрежем елемента abcdравнини, успоредни на оста zи наклонени под ъгъл 45° спрямо осите хИ при(фиг. 3). Както следва от условията на равновесие на елемент 0 bс, нормален стрес σ vпо всички страни на елемента abcdса равни на нула, а напреженията на срязване са равни

Това състояние на напрежение се нарича чисто срязване. От уравнения (5.2а) следва, че

тоест разширението на хоризонталния елемент е 0 ° Сравно на скъсяването на вертикалния елемент 0 b: εy = -εx.

Ъгъл между лицата абИ пр.н.епромени и съответната стойност на деформация на срязване γ може да се намери от триъгълник 0 bс:

Следва, че

Действието на външни сили върху твърдото тяло води до възникване на напрежения и деформации в точки от неговия обем. В този случай напрегнатото състояние в дадена точка, връзката между напреженията върху различни области, преминаващи през тази точка, се определят от уравненията на статиката и не зависят от физичните свойства на материала. Деформираното състояние, връзката между преместванията и деформациите, се установяват чрез геометрични или кинематични съображения и също не зависят от свойствата на материала. За да се установи връзка между напреженията и деформациите, е необходимо да се вземат предвид действителните свойства на материала и условията на натоварване. Въз основа на експериментални данни са разработени математически модели, описващи връзките между напрежения и деформации. Тези модели трябва да отразяват действителните свойства на материалите и условията на натоварване с достатъчна степен на точност.

Най-често срещаните модели за структурни материали са еластичността и пластичността. Еластичността е свойството на тялото да променя формата и размера си под въздействието на външни натоварвания и да възстановява първоначалната си конфигурация при премахване на товара. Математически свойството еластичност се изразява в установяването на функционална връзка едно към едно между компонентите на тензора на напрежението и тензора на деформацията. Свойството на еластичност отразява не само свойствата на материалите, но и условията на натоварване. За повечето структурни материали свойството на еластичност се проявява при умерени стойности на външни сили, водещи до малки деформации, и при ниски скорости на натоварване, когато загубите на енергия поради температурни ефекти са незначителни. Един материал се нарича линейно еластичен, ако компонентите на тензора на напрежението и тензора на деформацията са свързани с линейни зависимости.

При високи нива на натоварване, когато в тялото се появят значителни деформации, материалът частично губи своите еластични свойства: когато е разтоварен, първоначалните му размери и форма не се възстановяват напълно, а когато външните натоварвания са напълно премахнати, се записват остатъчни деформации. В такъв случай връзката между напреженията и деформациите престава да бъде еднозначна. Това материално свойство се нарича пластичност.Остатъчните деформации, натрупани по време на пластичната деформация, се наричат ​​пластични.

Високите нива на натоварване могат да причинят унищожаване, т.е. разделяне на тялото на части.Твърдите тела, направени от различни материали, се разрушават при различна степен на деформация. Счупването е крехко при малки деформации и по правило протича без забележими пластични деформации. Такова разрушаване е типично за чугун, легирани стомани, бетон, стъкло, керамика и някои други конструкционни материали. Нисковъглеродните стомани, цветните метали и пластмасите се характеризират с пластичен тип повреда при наличие на значителни остатъчни деформации. Въпреки това, разделянето на материалите на крехки и пластични според естеството на тяхното разрушаване е много произволно, обикновено се отнася до някои стандартни условия на работа. Един и същ материал може да се държи в зависимост от условията (температура, естеството на натоварването, технологията на производство и т.н.) като крехък или пластичен. Например, материали, които са пластични при нормални температури, се разпадат като крехки при ниски температури. Следователно е по-правилно да се говори не за крехки и пластични материали, а за крехко или пластично състояние на материала.

Нека материалът е линейно еластичен и изотропен. Нека разгледаме елементарен обем при условия на едноосно напрегнато състояние (фиг. 1), така че тензорът на напрежението да има формата

При такова натоварване размерите се увеличават по посока на оста охарактеризиращ се с линейна деформация, която е пропорционална на големината на напрежението

Фиг. 1.Едноосно напрегнато състояние

Тази връзка е математическа нотация Закон на Хукустановяване на пропорционална връзка между напрежението и съответната линейна деформация в състояние на едноосно напрежение. Коефициентът на пропорционалност E се нарича надлъжен модул на еластичност или модул на Юнг.Има измерението на стреса.

Заедно с увеличаването на размера в посока на действие; При едно и също напрежение се получава намаляване на размера в две ортогонални посоки (фиг. 1). Означаваме съответните деформации с и и тези деформации са отрицателни, докато положителни и са пропорционални на:

При едновременно действие на напрежения по три ортогонални оси, когато няма тангенциални напрежения, принципът на суперпозиция (суперпозиция на решения) е валиден за линейно еластичен материал:

Като вземем предвид формулите (1 4) получаваме

Тангенциалните напрежения причиняват ъглови деформации и при малки деформации не влияят на промяната на линейните размери и следователно на линейните деформации. Следователно те са валидни и при произволно напрегнато състояние и изразяват т.нар обобщен закон на Хук.

Ъгловата деформация се предизвиква от тангенциалното напрежение, а деформацията и съответно от напреженията и. Съществуват пропорционални връзки между съответните тангенциални напрежения и ъглови деформации за линейно еластично изотропно тяло

които изразяват закона Ножица на Хук.Коефициентът на пропорционалност G се нарича срязващ модул.Важно е нормалното напрежение да не влияе на ъгловите деформации, тъй като в този случай се променят само линейните размери на сегментите, а не ъглите между тях (фиг. 1).

Съществува линейна връзка и между средното напрежение (2.18), пропорционално на първия инвариант на тензора на напрежението, и обемната деформация (2.32), съвпадаща с първия инвариант на тензора на напрежението:

Съответен фактор на пропорционалност ДА СЕНаречен обемен модул на еластичност.

Формулите (1 7) включват еластичните характеристики на материала Д, , ЖИ ДА СЕ,определяне на неговите еластични свойства. Тези характеристики обаче не са независими. За изотропен материал има две независими еластични характеристики, които обикновено се избират като еластичен модул ди коефициент на Поасон. За изразяване на модула на срязване Жпрез дИ , Нека разгледаме равнинната деформация на срязване под действието на тангенциални напрежения (фиг. 2). За да опростим изчисленията, използваме квадратен елемент със страна А.Нека изчислим главните напрежения , . Тези напрежения действат върху области, разположени под ъгъл спрямо първоначалните области. От фиг. 2 ще намерим връзката между линейната деформация в посока на напрежението и ъгловата деформация . Големият диагонал на ромба, характеризиращ деформацията, е равен на

За малки деформации

Отчитайки тези отношения

Преди деформацията този диагонал имаше размера . Тогава ще имаме

От обобщения закон на Хук (5) получаваме

Сравнението на получената формула с нотацията на закона на Хук за отместване (6) дава

В резултат на това получаваме

Сравнявайки този израз с обемния закон на Хук (7), стигаме до резултата

Механични характеристики Д, , ЖИ ДА СЕса открити след обработка на експериментални данни от тестови проби при различни видове натоварвания. От физическа гледна точка всички тези характеристики не могат да бъдат отрицателни. В допълнение, от последния израз следва, че коефициентът на Поасон за изотропен материал не надвишава 1/2. Така получаваме следните ограничения за еластичните константи на изотропен материал:

Граничната стойност води до гранична стойност , което съответства на несвиваем материал (at). В заключение, от отношенията на еластичност (5) изразяваме напрежението по отношение на деформация. Нека запишем първото от отношенията (5) във формата

Използвайки равенство (9), ще имаме

Подобни зависимости могат да се изведат за и . В резултат на това получаваме

Тук използваме връзка (8) за модула на срязване. Освен това обозначението

ПОТЕНЦИАЛНА ЕНЕРГИЯ НА ЕЛАСТИЧНА ДЕФОРМАЦИЯ

Нека първо разгледаме елементарния обем dV=dxdydzпри условия на едноосно напрежение (фиг. 1). Психически оправете сайта х=0(фиг. 3). Върху противоположната повърхност действа сила . Тази сила работи върху изместването . Когато напрежението се увеличи от нулево ниво до стойността съответната деформация поради закона на Хук също нараства от нула до стойността , и работата е пропорционална на защрихованата фигура на фиг. 4 квадрата: . Ако пренебрегнем кинетичната енергия и загубите, свързани с топлинни, електромагнитни и други явления, тогава, поради закона за запазване на енергията, извършената работа ще се превърне в потенциална енергия,натрупани по време на деформация: . Стойност Ф= dU/dVНаречен специфична потенциална енергия на деформация,имащ смисъл на потенциална енергия, натрупана в единица обем на тяло. При едноосно напрегнато състояние